Blog Sobre mí Contacto Iniciar Sesión Registro
Inicio Machine Learning Modelos de regresión lineal simple con Python

Modelos de regresión lineal simple con Python

La regresión lineal simple es un modelo de Machine Learning para predecir la relación existente entre variables, es decir, la relación que hay entre datos. Esto nos proporcionará un método rápido y sencillo para comprender la influencia entre variables, verificando si al aumentar el valor de una lo hace la otra o si, en caso contrario, al disminuir el valor de la variable la otra también decae.

La regresión lineal simple es un modelo de aprendizaje automático supervisado para realizar predicciones sobre datos continuos, permitiendo que tracemos una línea sobre los datos. Esta "línea" puede ser recta, con picos o con formas redondeadas, pero mantendrá la continuidad en el gráfico resultante.

En este artículo vamos a crear una regresión lineal en Python para un modelo de Machine Learning en donde utilizaremos datos de facturación de clientes. El objetivo es poder predecir la facturación de un nuevo cliente.
  • Índice Regresión Lineal Simple con Python:

Para poder comprender el alcance de la regresión y sus ventajas antes de implementar el código Python, es importante comprender todas sus características y funcionalidades. Como comprobarás, el código generado es bastante sencillo, pero como indico, más allá de su extensión, la importancia radica en su comprensión para poder sacar conclusiones del conjunto de datos y, posteriormente poder implementar este modelo ML en muchas situaciones.

Qué es una regresión lineal

Hay diferentes tipos de regresión lineal, y la más sencilla y práctica para aprender machine learning es la regresión lineal simple. Esta consta de una variable independiente y otra variable dependiente, pudiendo existir una relación entre ambas variables que hará que, a medida que aumenta el valor de una la otra lo haga proporcionalmente.

En estadística la regresión lineal simple o el ajuste lineal es un modelo matemático utilizado para encontrar la relación de dependencia entre una variable dependiente (y) y otra independiente (X). En el caso de la regresión lineal múltiple buscaría la relación entre una variable dependiente y m variable independientes.

Código regresión lineal simple con Python

Vamos a ir generando el código de la regresión lineal simple paso a paso para una mejor compresión y, al final de los ejemplos, estará el código Python completo de la regresión lineal simple por si lo quieres copiar y modificar para lo que necesites.

Generamos un dataframe pandas con los datos de cliente

import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# ------------------------------------
# Crear dataframe con los datos de facturación de clientes
data = {'customer_id': [1, 2, 3, 4, 5],
        'billing_amount': [100, 200, 150, 300, 250],
        'sales': [2, 4, 3, 6, 5]
}
clients = pd.DataFrame(data)

Mostrar los datos del dataframe pandas

A continuación, mostramos los datos almacenados en el dataframe: 
print(clients)
El dataframe clientes (clients) contiene: 

---------------------------------
Dataframe clients contiene:
---------------------------------
   customer_id  billing_amount  sales
0            1             100      2
1            2             200      4
2            3             150      3
3            4             300      6
4            5             250      5
---------------------------------
Con esto ya tendríamos cargados los datos de clientes en el dataframe, recuerda que es similar a un array en otros lenguajes de programación. Podríamos continuar, pero antes de seguir con la regresión lineal, vamos a comprobar los tipos de datos contenidos en el conjunto de datos y las dimensiones dataframe 
print(clients.info())

---------------------------------
Visualizar los tipos de datos de clients:
---------------------------------

RangeIndex: 5 entries, 0 to 4
Data columns (total 3 columns):
 #   Column          Non-Null Count  Dtype
---  ------          --------------  -----
 0   customer_id     5 non-null      int64
 1   billing_amount  5 non-null      int64
 2   sales           5 non-null      int64
dtypes: int64(3)
memory usage: 248.0 bytes
None

Mostrar el número de dimensiones del dataframe

las dimensiones del dataframe y el conjunto de datos las necesitaremos para el entrenamiento de nuestro modelo de Machine Learning cuando vayamos a crear la regresión lineal. Aunque en un principio no es necesario conocer las dimensiones, siempre es bueno acostumbrarse a mostrarlas por pantalla y, en caso necesario, usar el comando python. 
print(clients.shape)

---------------------------------
Número de dimensiones del dataframe clients:
---------------------------------
(5, 3)

Creación de los conjuntos de entrenamiento y prueba

X_train, X_test, y_train, y_test = train_test_split(clients['billing_amount'], clients['sales'], random_state=20)
Con esta línea de código indicamos que se cree, genere y divida los datos de cliente en varios conjuntos de datos de entrenamiento y prueba:
  • Datos de entrada: 'customer_id'.
  • Variable dependiente:'billing_amount, que es el importe de facturación del cliente.
  • ramdom_state: indica que se cree una semilla aleatoria para dividir los datos de forma consistente cada vez que ejecutamos el código.
  • X_train: representa los datos de entrada del conjunto de entrenamiento, es decir, los datos que se utilizarán para entrenar el modelo.
  • X_test: representa los datos de entrada del conjunto de prueba, es decir, los datos que se utilizarán para evaluar el rendimiento del modelo entrenado.
  • y_train: representa los datos de salida del conjunto de entrenamiento, es decir, los datos objetivo que se utilizarán para entrenar el modelo.
  • y_test: representa los datos de salida del conjunto de prueba, es decir, los datos objetivo que se utilizarán para evaluar el rendimiento del modelo entrenado.
Dividir los datos en un conjunto de entrenamiento y un conjunto de prueba es importante para poder evaluar el rendimiento del modelo entrenado con datos en Machine Learning.

Creación regresión linear simple

Y creamos la regresión linear simple con una sola línea de python. 
lr = LinearRegression().fit(X_train.values.reshape(-1, 1), y_train)

Creación predicción con datos de test

Ahora creamos una predicción con nuestro modelo entrenado. Para ello le pasamos los datos de prueba que previamente habíamos generado de forma automática para que dividiera los datos de forma equivalente y no tuviéramos más datos para entrenamiento o pruebas. 
y_pred = lr.predict(X_test.values.reshape(-1, 1))
NOTA: X_test contiene los datos de entrada de prueba. Añadir ".reshape(-1, 1)" o ".values.reshape(-1, 1)" es para redimensionar la matriz a las dimensiones que requiere el módulo de Python LinearRegresion(). Según el conjunto de datos utilizado, podremos añadir directamente la variable o será necesario redimensionarla con reshape o con values.reshape.

Mostramos los coeficientes mínimos cuadrados W1 y W0

print("Coeficiente w1:", lr.coef_)
print("Coeficiente w0:", lr.intercept_)

Coeficiente w1: [0.02]
Coeficiente w0: 4.440892098500626e-16

Error cuadrático medio

El error cuadrático medio (ECM) o RMSE) mide la diferencia al cuadrado entre el valor real y el valor predicho en el total de predicciones de nuestro modelo de Machine Learning. Muestra las diferencias más elevadas. 
print(mean_squared_error(y_test, y_pred))

0.0

En estadística, el error cuadrático medio es un estimador que mide el promedio de errores al cuadrado, es decir, la diferencia entre el estimador y lo que se estima. Es un parámetro perfecto para medir la cantidad de error entre dos conjuntos de datos. Una explicación sencilla es decir que compara el valor predicho con el valor conocido, dando como resultado un coeficiente de error.

NOTA: un valor vajo de RMSE indica un mejor ajuste del modelo.

Coeficientes de determinación

print("Valor del coeficiente de determinación del conjunto de entrenamiento:", (lr.score(X_train.values.reshape(-1, 1), y_train), 3))
print("Valor del coeficiente de determinación del conjunto de prueba:", round(lr.score(X_test.values.reshape(-1, 1), y_test), 3))

Valor del coeficiente de determinación del conjunto de entrenamiento: (1.0, 3)
Valor del coeficiente de determinación del conjunto de prueba: 1.0

El coeficiente de determinación de entrenamiento y de pruebas debe ser parecido. Cuando encontramos que ambos valores tienen una diferencia grande suele significar que el modelo está mal ajustado. El coeficiente de determinación (R2) (R al cuadrado) se utiliza en estadística para cuantificar cómo de cerca están los puntos en la recta de regresión.

Salidas gráfica de regresión lineal simple

import seaborn as sns
import matplotlib.pyplot as plt

# Crear un gráfico de regresión lineal usando seaborn
sns.lmplot(x='sales', y='billing_amount', data=clients)
# Mostrar gráfico
plt.show()

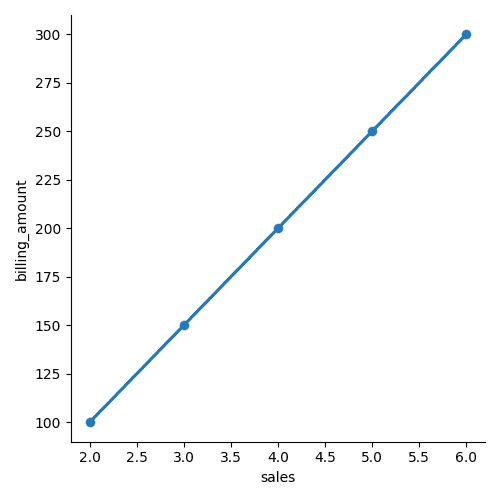
Y esto genera la gráfica siguiente:

Regresión lineal con Python con librería matplotlib plot y seaborn

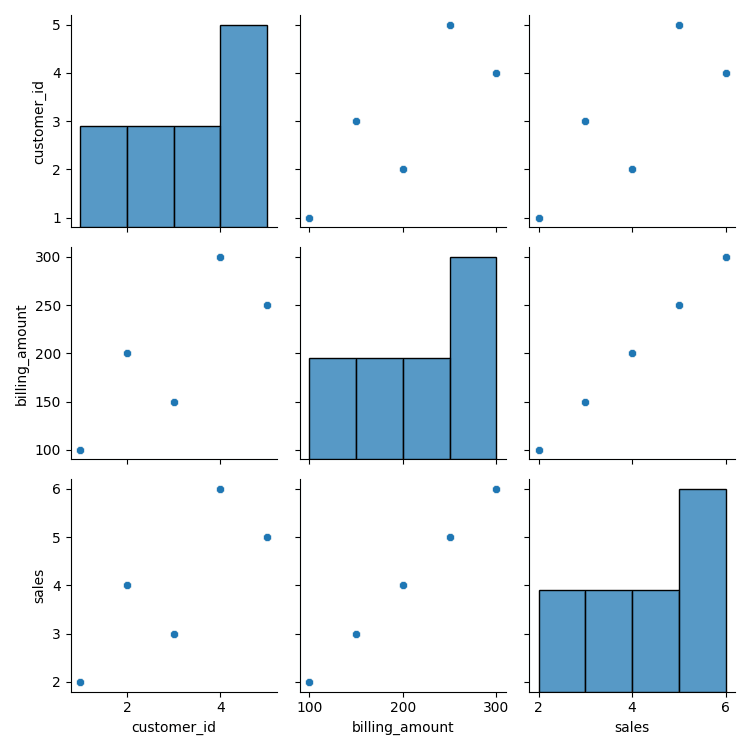
Gráfica de relación entre variables del conjunto de datos

# Gráfico de relación entre variables del conjunto de datos.
sns.pairplot(clients, height=2.5)
plt.tight_layout()
plt.show()
La salida gráfica es la siguiente:
Gráfico de relación entre variables del conjunto de datos

Gráfica de datos de entrenamiento

# Graficando los datos de entrenamiento
plt.scatter(X_train, y_train, color='blue')

# Grafica de la regresión lineal con datos de la predicción
plt.plot(X_test, y_pred, color='red')
plt.title('Regresión Lineal Simple')
plt.xlabel('Importe de facturación')
plt.ylabel('Ventas')
plt.show()
Y genera el gráfico siguiente:
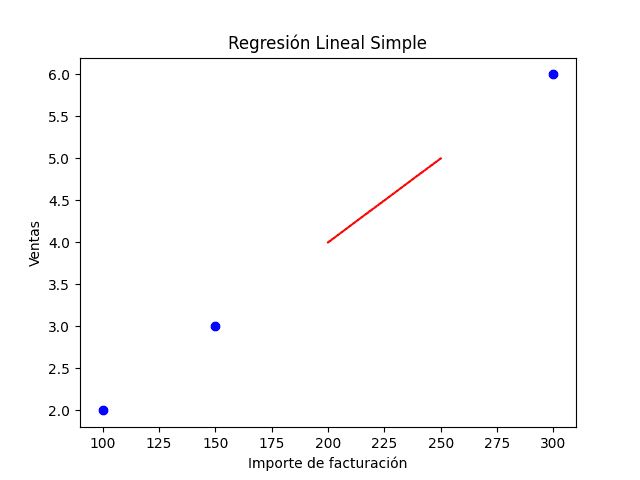
Gráfica de datos de entrenamiento

Con esto ya tenemos creada una regresión lineal simple con Python. Si quieres el script completo, a continuación lo tienes disponible.

Esta gráfica, la última, muestra los puntos de los datos de entrenamiento en color azul y la línea de regresión lineal en rojo.

La línea de regresión lineal representa el modelo que se ha entrenado para hacer predicciones.

La interpretación de la gráfica indica que, a medida que el número de ventas se incrementa, el importe de facturación también aumenta. Esto se ve reflejado en la pendiente positiva de la línea de regresión. Sin embargo, esta es una interpretación basada en una sola variable, si se utilizaran más variables se podría tener una interpretación más precisa y completa.
 

Código completo regresión lineal simple con Python

Aquí está todo el código Python de la regresión lineal simple. Para aplicarla a tus propios datos, solo tendrás que modificar la creación del dataframe pandas, añadiendo tu propio conjunto de datos o importándolos con pandas desde un archivo csv o desde Excel y otros formatos de archivos de datos. 
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# ------------------------------------
# Crear dataframe con los datos de facturación de clientes
data = {'customer_id': [1, 2, 3, 4, 5],
        'billing_amount': [100, 200, 150, 300, 250],
        'sales': [2, 4, 3, 6, 5]
}
clients = pd.DataFrame(data)

# Mostramos los datos asignados a las variables para luego usar la regresión.
print('\n---------------------------------')
print('Dataframe clients contiene:')
print('---------------------------------')
print(clients)
print('---------------------------------')

print('\n---------------------------------')
print('Visualizar los tipos de datos de clients:')
print('---------------------------------')
print(clients.info())


print('\n---------------------------------')
print('Número de dimensiones del dataframe clients:')
print('---------------------------------')
print(clients.shape)


print('\n---------------------------------')
print('Asignación de los valores a las variables X e y:')
print('---------------------------------')
X = clients['billing_amount']
y = clients['sales']

print('\n---------------------------------')
print('X contiene:')
print('---------------------------------\n')
print(X)
print('\n---------------------------------')
print('y contiene:')
print('---------------------------------\n')
print(y)


# Creación de los conjuntos de entrenamiento y de prueba
X_train, X_test, y_train, y_test = train_test_split(clients['billing_amount'], clients['sales'], random_state=20)


print('\n---------------------------------')
print('Nº dimensiones de X_train:')
print('---------------------------------\n')
print(X_train.shape)
print('\n---------------------------------')
print('Nº dimensiones de y_train:')
print('---------------------------------\n')
print(y_train.shape)

# Creación regresión linear simple
lr = LinearRegression().fit(X_train.values.reshape(-1, 1), y_train)

# Creación de la predicción
y_pred = lr.predict(X_test.values.reshape(-1, 1))

# Mostramos los coeficientes W1 y W0.
print('\n---------------------------------')
print('Coeficientes de mínimos cuadrados W1 y W0:')
print('---------------------------------')
print("Coeficiente w1:", lr.coef_)
print("Coeficiente w0:", lr.intercept_)


# Valor del error cuadrático medio.
# Compara los valores del conjunto de prueba con los predichos por el modelo entrenado.
print('\n---------------------------------')
print('Error cuadrático medio::')
print('---------------------------------')
print(mean_squared_error(y_test, y_pred))

# Valores del coeficiente de determinación
print("Valor del coeficiente de determinación del conjunto de entrenamiento:", (lr.score(X_train.values.reshape(-1, 1), y_train), 3))
print("Valor del coeficiente de determinación del conjunto de prueba:", round(lr.score(X_test.values.reshape(-1, 1), y_test), 3))


# Salidas gráficas
import seaborn as sns
import matplotlib.pyplot as plt

# Crear un gráfico de regresión lineal usando seaborn
sns.lmplot(x='sales', y='billing_amount', data=clients)

# Mostrar gráfico
plt.show()

# Gráfico de relación entre variables del conjunto de datos.
sns.pairplot(clients, height=2.5)
plt.tight_layout()
plt.show()

# Graficando los datos de entrenamiento
plt.scatter(X_train, y_train, color='blue')

# Grafica de la regresión lineal con datos de la predicción
plt.plot(X_test, y_pred, color='red')
plt.title('Regresión Lineal Simple')
plt.xlabel('Importe de facturación')
plt.ylabel('Ventas')
plt.show()
Espero que con este código python de regresión lineal simple hayas comprendido como realizar las tuyas propias.

Si quieres aprender más sobre aprendizaje automático, puedes ver los diferentes modelos de Machine Learning supervisado.
Machine Learning

Comentarios del artículo "Modelos de regresión lineal simple con Python"

¿Te ha gustado la información? Coméntanos tus opiniones, dudas y sugerencias:

Añade un comentario:

Tu dirección de correo electrónico no será publicada. | Registro requerido. | ¿Ya eres usuario? Login