Modelos de Regresión Lineal Múltiple con Python
La regresión lineal múltiple es una técnica de Machine Learning para predecir la relación existente entre varias variables independientes y una única variable dependiente y su implementación puede realizarse con Python.
Este modelo de aprendizaje supervisado de Machine Learning tiene una serie de ventajas sobre la regresión lineal simple, como poder realizar predicciones sobre dos variables o más, teniendo como objetivo reducir las diferencias entre los valores reales y los que predice el modelo.
La representación de la ecuación ahora es un hiperplano en un espacio n-dimensional. Recuerda que en el modelo simple es un plano bidimensional.
La representación de la ecuación ahora es un plano en lugar de una recta, es decir, pasa de ser un plano bidimensional en el modelo simple a un hiperplano en un espacio n-dimensional.
Su objetivo es encontrar lo coeficientes que mejor ajustan los datos y que permite realizar predicciones más precisas sobre la variable dependiente a partir de los datos o variables independientes.
En este ejemplo hemos creado un conjunto de datos sencillo para facilitar la explicación de cómo crear un análisis de regresión lineal múltiple programado en Python.
Y el resultado lo mostramos por pantalla:
Es bastante frecuente que el problema del sesgo esté influenciado por un conjunto de datos simple en la regresión lineal, como sucede en este caso que estamos tratando.
Cuando ya tenemos el código Python con el entrenamiento del modelo de la regresión múltiple y hemos calculado los coeficientes de determinación, el error cuadrático medio y el posible sesgo del algoritmo de ML, es el momento de mostrar los datos en una gráfica.
Y estas líneas de código generarán el siguiente gráfico:
En este ejemplo estamos creando una gráfica con la relación entre la variable dependiente Y (billing_amount) y una de las variables independientes X (sales), pero podríamos realizar cualquier otra relación con las variables del conjunto de datos. Ten en cuenta que no usamos customer_id ya que esta es una variable categórica o discreta y no tendría sentido implementarla. Por sí solo, el id del cliente no indica nada más allá de ser un número identificativo que, generalmente es creada de forma automática e incremental, pero su valor no indica ningún tipo de relación que nos pueda interesar.
El código Python de la regresión lineal múltiple da como resultado lo siguiente:
Después de imprimir estos valores, generará el gráfico. ¡Y eso es todo!
También puedes ver cómo crear una regresión lineal simple con Python, un ejemplo mucho más sencillo y que te recomiendo que hagas primero para avanzar con tus conocimientos de aprendizaje automático supervisado.
Este modelo de aprendizaje supervisado de Machine Learning tiene una serie de ventajas sobre la regresión lineal simple, como poder realizar predicciones sobre dos variables o más, teniendo como objetivo reducir las diferencias entre los valores reales y los que predice el modelo.
- Índice Regresión Lineal Múltiple con Python:
Qué es una regresión múltiple
Muy usada en ciencias de la computación para el tratamiento de grandes conjuntos de datos, la regresión lineal múltiple es un modelo estadístico que sirve para evaluar las relaciones entre varias variables independientes (X1, X2, X3,...) llamados predictores y una variable dependiente (Y) o valor de salida.La representación de la ecuación ahora es un hiperplano en un espacio n-dimensional. Recuerda que en el modelo simple es un plano bidimensional.
La representación de la ecuación ahora es un plano en lugar de una recta, es decir, pasa de ser un plano bidimensional en el modelo simple a un hiperplano en un espacio n-dimensional.
Su objetivo es encontrar lo coeficientes que mejor ajustan los datos y que permite realizar predicciones más precisas sobre la variable dependiente a partir de los datos o variables independientes.
Diferencias entre regresión lineal múltiple y simple
Independientemente de su campo de aplicación (estadística, informática o ciencias de la información, Marketing, etc.), la regresión lineal múltiple es un modelo estadístico que amplía la funcionalidad de la regresión lineal simple. Esta última, la simple, solo puede predecir las relaciones entre dos variables. En cambio, la regresión múltiple permite predecir las relaciones existentes entre dos o más variables entendiendo que analiza la variabilidad de la variable dependiente mediante la combinación lineal de varias variables independientes.
Código regresión lineal múltiple con Python
Obtener datos
Lo primero es obtener los datos que vamos a procesar con nuestro modelo de ML. Para ello, vamos a crear un dataframe pandas, pero también puedes obtener el conjunto de datos de un archivo csv que suele ser lo más frecuente en un entorno de desarrollo real:
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
# Crear dataframe con los datos de facturación de clientes
data = {'customer_id': [1, 2, 3, 4, 5],
'billing_amount': [100, 200, 150, 300, 250],
'sales': [2, 4, 3, 6, 5],
'customer_since': [2010, 2012, 2014, 2016, 2018],
'age': [35, 40, 45, 30, 25],
'gender': ['M', 'F', 'M', 'F', 'M']
}
clients = pd.DataFrame(data)
Asignación de los valores a X e y: variable independiente y variable dependiente.
Ahora vamos a indicar cuáles son los valores que debe tomar cada variable del modelo.
# Seleccionar las variables independientes (X) y la variable dependiente (y).
X = clients[['sales', 'customer_since', 'age']]
y = clients['billing_amount']
Podemos elegir cuáles son los datos de estas variables en su creación, es decir, que no tienen por qué ser los indicados, sino que, en cada tipo de caso seleccionar las etiquetas, columnas o valores que vamos a necesitar para nuestro modelo ML.
Creación del conjunto de datos de entrenamiento y conjunto de prueba
Indicamos cómo deben repartirse los datos que hemos obtenido.
# Dividir los datos en conjunto de entrenamiento y conjunto de prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
Explicación:
- train_test_split: le pasamos las variables (X, y) que han sido creadas con los datos deseados del dataframe.
- test_size: es el tamaño del conjunto de test del algoritmo pudiendo tener un valor entre 0.0 y 1.0. Por defecto test_size = 0.25. Podemos modificarlo según nuestros intereses en cada modelo. Si indicamos un número entero, test_size indicará el número de muestras que empleará en la evaluación. Si test_size = 10, el conjunto de test tomará 10 datos de muestra y el resto de datos será enviado a entrenamiento del modelo. Por ejemplo: tenemos un conjunto de datos con 100 valores. test_size = 20. En este caso, 20 valores son enviados al conjunto de test y 80 valores a entrenamiento.
Entrenamiento del modelo
Con la siguiente línea de código estamos indicando que entrene el modelo de regresión lineal múltiple con el conjunto de datos de entrenamiento de las variables independientes y la variable dependiente. Recuerda que previamente las creamos con train_test_split.
# Crear el modelo de regresión lineal múltiple
reg = LinearRegression().fit(X_train, y_train)
Creación de la predicción
Con el método predict podemos realizar predicciones. En este caso le pasamos como parámetro datos de las variables independientes de test, es decir, los datos para hacer pruebas.
# Hacer predicciones sobre el conjunto de prueba
y_pred = reg.predict(X_test)
Cálculo de error cuadrático medio
También es importante conocer las posibles diferencias entre las estimaciones realizadas y los valores reales y, en este caso, usamos el error cuadrático medio.
# Calcular el error cuadrático medio
mse = mean_squared_error(y_test, y_pred)
print("Error cuadrático medio:", mse)
Cálculo de coeficiente de determinación y sesgo
El sesgo o bias de un algoritmo de machine learning es la tendencia del modelo a tomar decisiones poco exactas, es decir, realizar predicciones incorrectas debido a patrones en los datos de entrenamiento, motivo por el cual es importante conocerlo.
# Imprimir los coeficientes y el sesgo - Valores de los pesos del modelo de regresión
print("Coeficientes:", reg.coef_)
print("Sesgo (Coeficiente W0:", reg.intercept_)
print("Coeficiente W1:", reg.coef_[0])
print("Coeficiente W2:", reg.coef_[1])
# Imprimir el coeficientes de determinación
print("Coeficiente de determinación:", reg.score(X_train, y_train))
Error cuadrático medio: 6.54312789226516e-26
Coeficientes: [ 5.00000000e+01 8.17526121e-14 -5.83114209e-15]
Sesgo (Coeficiente W0): -1.637943114474183e-10
Coeficiente W1: 49.99999999999982
Coeficiente W2: 8.175261214579157e-14
Coeficiente de determinación: 1.0
Cuando ya tenemos el código Python con el entrenamiento del modelo de la regresión múltiple y hemos calculado los coeficientes de determinación, el error cuadrático medio y el posible sesgo del algoritmo de ML, es el momento de mostrar los datos en una gráfica.
Crear gráfico de la regresión lineal múltiple con Python matplotlib
Para mostrar los datos de la regresión lineal múltiple en Python usaremos la biblioteca matplotlib y su módulo pyplot.
# Salida gráfica
# Crear una figura y un eje
fig, ax = plt.subplots()
# Graficar los puntos de entrenamiento
ax.scatter(X_train['sales'], y_train, color='blue', label='Entrenamiento')
# Graficar los puntos de prueba
ax.scatter(X_test['sales'], y_test, color='red', label='Prueba')
# Graficar la recta de regresión
ax.plot(X_test['sales'], y_pred, color='black', linewidth=2, label='Regresión')
# Agregar etiquetas al eje X e Y
ax.set_ylabel("billing_amount")
ax.set_xlabel("sales")
# Agregar un título al gráfico
ax.set_title("Regresión lineal múltiple")
# Mostrar la leyenda
ax.legend()
# Mostrar el gráfico
plt.show()
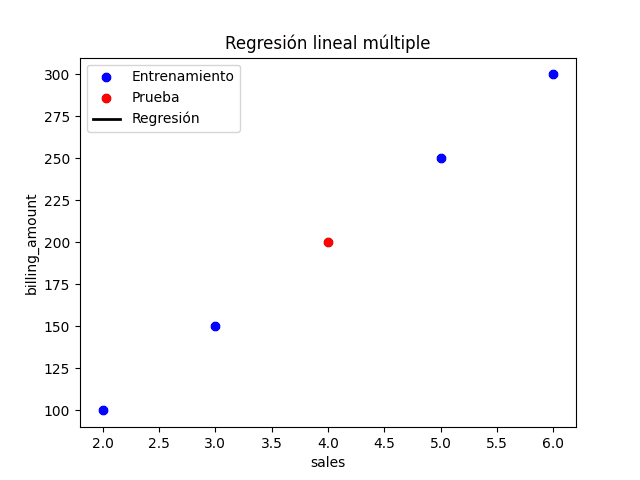
En este ejemplo estamos creando una gráfica con la relación entre la variable dependiente Y (billing_amount) y una de las variables independientes X (sales), pero podríamos realizar cualquier otra relación con las variables del conjunto de datos. Ten en cuenta que no usamos customer_id ya que esta es una variable categórica o discreta y no tendría sentido implementarla. Por sí solo, el id del cliente no indica nada más allá de ser un número identificativo que, generalmente es creada de forma automática e incremental, pero su valor no indica ningún tipo de relación que nos pueda interesar.
Código completo regresión lineal múltiple con Python
Finalizada la explicación paso a paso sobre cómo crear una regresión lineal múltiple mediante python, te dejo el código completo para que sea mucho más sencillo estudiar en tus propios modelos de ML.
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
# Crear dataframe con los datos de facturación de clientes
data = {'customer_id': [1, 2, 3, 4, 5],
'billing_amount': [100, 200, 150, 300, 250],
'sales': [2, 4, 3, 6, 5],
'customer_since': [2010, 2012, 2014, 2016, 2018],
'age': [35, 40, 45, 30, 25],
'gender': ['M', 'F', 'M', 'F', 'M']
}
clients = pd.DataFrame(data)
# Seleccionar las variables independientes (X) y la variable dependiente (y).
X = clients[['sales', 'customer_since', 'age']]
y = clients['billing_amount']
# Dividir los datos en conjunto de entrenamiento y conjunto de prueba
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Crear el modelo de regresión lineal múltiple
reg = LinearRegression().fit(X_train, y_train)
# Hacer predicciones sobre el conjunto de prueba
y_pred = reg.predict(X_test)
# Calcular el error cuadrático medio
mse = mean_squared_error(y_test, y_pred)
print("Error cuadrático medio:", mse)
# Imprimir los coeficientes y el sesgo - Valores de los pesos del modelo de regresión
print("Coeficientes:", reg.coef_)
print("Sesgo (Coeficiente W0:", reg.intercept_)
print("Coeficiente W1:", reg.coef_[0])
print("Coeficiente W2:", reg.coef_[1])
# Imprimir el coeficientes de determinación
print("Coeficiente de determinación:", reg.score(X_train, y_train))
# Salida gráfica
# Crear una figura y un eje
fig, ax = plt.subplots()
# Graficar los puntos de entrenamiento
ax.scatter(X_train['sales'], y_train, color='blue', label='Entrenamiento')
# Graficar los puntos de prueba
ax.scatter(X_test['sales'], y_test, color='red', label='Prueba')
# Graficar la recta de regresión
ax.plot(X_test['sales'], y_pred, color='black', linewidth=2, label='Regresión')
# Agregar etiquetas al eje X e Y
ax.set_ylabel("billing_amount")
ax.set_xlabel("sales")
# Agregar un título al gráfico
ax.set_title("Regresión lineal múltiple")
# Mostrar la leyenda
ax.legend()
# Mostrar el gráfico
plt.show()
Error cuadrático medio: 6.54312789226516e-26
Coeficientes: [ 5.00000000e+01 8.17526121e-14 -5.83114209e-15]
Sesgo (Coeficiente W0): -1.637943114474183e-10
Coeficiente W1: 49.99999999999982
Coeficiente W2: 8.175261214579157e-14
Coeficiente de determinación: 1.0
También puedes ver cómo crear una regresión lineal simple con Python, un ejemplo mucho más sencillo y que te recomiendo que hagas primero para avanzar con tus conocimientos de aprendizaje automático supervisado.
Comentarios del artículo "Modelos de Regresión Lineal Múltiple con Python"
¿Te ha gustado la información? Coméntanos tus opiniones, dudas y sugerencias: