Correlación de variables con Pandas .corr()
Pandas es una biblioteca de Python para el análisis de datos. Uno de los principales componentes de Pandas es el DataFrame, que es una estructura de datos en forma de tabla con filas y columnas. El método .corr() en un DataFrame de Pandas se utiliza para calcular la correlación entre las columnas numéricas del DataFrame. La correlación es una medida estadística que indica la relación lineal entre dos variables. El valor de la correlación varía entre -1 y 1, donde -1 indica una correlación negativa perfecta, 0 indica que no hay correlación y 1 indica una correlación positiva perfecta.
El resultado obtenido con el método corr de pandas es un DataFrame con las correlaciones entre todas las columnas numéricas del DataFrame original. Cada celda contiene la correlación entre las dos columnas correspondientes.
Esto nos dará el valor de la correlación entre las dos variables o columnas.
El resultado será la impresión por pantalla de todos los valores de las correlaciones entre las columnas o variables del dataframe, siendo mucho más recomendable utilizar este método que el de un único valor ya que, de esta forma, podremos analizar si existen otras correlaciones dentro del conjunto de datos con el que estamos trabajando.
En general, si las variables son continuas y se cree que siguen una distribución normal, Pearson es el algoritmo más recomendado para utilizar. En cambio, si las variables son ordinales o continuas pero pensamos que no tienen una distribución normal, Kendall o Spearman son algoritmos más recomendables.
La elección del algoritmo de correlación a utilizar depende del tipo de variables y de la distribución de las mismas.
Aunque mostremos los resultados de la correlación de variables por pantalla, suele ser mucho más eficaz exportar las correlaciones a un archivo .csv o .xlsx de Excel para poder trabajar con ellas y analizarlas de forma óptima. Para ello, solo debes realizar la exportación de los resultados de corr con los métodos habituales de pandas, es decir, para exportar a csv: dataframe.to_csv(ruta_exportación) y para excel: dataframe.to_excel(ruta_exportación).
Y lo siguiente es después de usar .info(), que es una forma sencilla de ver los tipos de datos almacenados dentro de las columnas del dataframe:
Y Ahora, el resultado final con la tabla de correlaciones al usar el método .corr() de pandas:
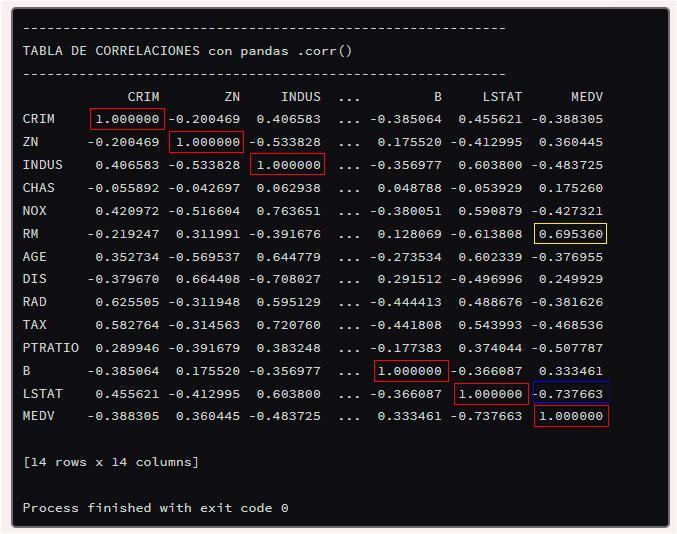
Los valores mostrados como -1 indican que las columnas están correlacionadas inversamente, es decir, a medida que una columna aumenta su valor en la otra disminuye y viceversa.
NOTA: recuerda que el método corr() solo funciona con datos numéricos. Si realizas la correlación con otro tipo de datos obtendrás NaN en la celda correspondiente, en cuyo caso, antes de implementarlo es conveniente aplicar los métodos dtypes o astype para convertir los valores a numéricos según sea el caso, siempre y cuando contengan números.
Siguiendo con la explicación e interpretación de los resultados de 'corr()' el ejemplo del dataset Boston, encontramos que hay algunas variables con un correlación fuerte como el caso de MEDV con RM ya que su valor es 0.695360. Dada la temática del conjunto de datos que está enfocada en el precio de la vivienda, descubrimos que cuantas más habitaciones tiene una vivienda, el precio de la misma es más elevado. Si el número de habitaciones aumenta (RM) el valor de MEDV también aumenta.
En el caso de las correlaciones inversas, podemos ver como MEDV y LSTAT están influenciadas inversamente con un valor -0.738, es decir, mostrando que el precio de la vivienda es menor cuando las personas que la habitan tienen una condición social baja. Si el valor de LSTAT aumenta el valor de MEDV disminuye. Si hay más individuos con baja condición social en la zona el precio de la vivienda cae.
En resumen, recuerda que los valores positivos en las correlaciones indican que si una variable aumenta su valor la otra lo hará también y, si el valor es negativo cuando aumenta el valor de la variable provoca que la otra variable disminuya su valor.
Antes de aplicar la regresión lineal es posible calcular la correlación entre la variable independiente y la variable dependiente para determinar si se debe continuar con el análisis. Si la correlación es alta y positiva, significa que hay una relación significativa entre las dos variables y se puede continuar con el análisis utilizando el modelo de regresión lineal. Si la correlación es baja o negativa, no hay una relación significativa entre las dos variables, no es necesario o no se recomienda continuar con el análisis utilizando el modelo de regresión lineal gracias a los datos mostrados con corr. Esto evitará pérdida de tiempo y costes innecesarios en desarrollos y minería de datos.
- Índice Correlación de variables Pandas corr():
Cómo usar pandas .corr()
Para usar el método .corr() en un DataFrame de Pandas, simplemente seleccionamos el DataFrame y llamamos al método. Por ejemplo, si tenemos un DataFrame llamado df, podemos calcular la correlación entre las columnas de la siguiente manera:
# Obtener correlación de las variables del DataFrame.
correlation = df.corr()
Cómo acceder a las correlaciones
Si queremos ver la correlación entre diferentes columnas, por ejemplo, la correlación existente entre las columnas "columna1" y "columna2", podemos acceder al valor correspondiente de la correlación entre esas columnas de la siguiente manera:
# Acceder al valor de la correlación de dos columnas
correlation['columna1']['columna2']
Mostrar todas las correlaciones del dataframe
Si en lugar de querer obtener un solo resultado deseamos visualizar todas las correlaciones entre las variables del dataframe, después de usar .corr() solo deberemos imprimirlo de la siguiente forma:
# Mostrar todas las correlaciones del dataframe.
print(data_corr.corr())
Opciones y métodos de .corr()
El método .corr() también admite argumentos opcionales:- method: permite especificar el algoritmo de cálculo de la correlación (por defecto es "pearson").
- pearson: coeficiente de correlación estándar. Este es el algoritmo por defecto y se utiliza para calcular la correlación de Pearson. Es una medida de la relación lineal entre dos variables y se basa en la covarianza entre ellas. Adecuado para variables continuas, asumiendo que ambas variables siguen una distribución normal.
- kendall: coeficiente de correlación Tau de kendall. Es una medida no paramétrica de la relación entre dos variables ordinales o continuas y se basa en el número de pares ordenados que tienen el mismo orden en ambas variables. Es adecuado para variables ordinales o continuas no necesariamente normales.
- spearman: correlación de rango de Spearman. Utiliziado para calcular la correlación de Spearman. Esta es una medida no paramétrica de la relación entre dos variables y se basa en la correlación entre las posiciones de las variables en un ranking. Es adecuado para variables ordinales o continuas no necesariamente normales.
- min_periods: indica el número mínimo de observaciones necesarias para calcular la correlación con un resultado válido (por defecto es 1). Solo puede utilizarse para la correlación con method pearson o sperman.
- numeric_only: bool, default True. Incluir solo datos flotantes, int o booleanos.
En general, si las variables son continuas y se cree que siguen una distribución normal, Pearson es el algoritmo más recomendado para utilizar. En cambio, si las variables son ordinales o continuas pero pensamos que no tienen una distribución normal, Kendall o Spearman son algoritmos más recomendables.
La elección del algoritmo de correlación a utilizar depende del tipo de variables y de la distribución de las mismas.
Exportar correlaciones
Lo datos contenidos en un dataframe pandas pueden ser exportados a múltiples tipos de archivos y, en el caso de 'corr()' también puede realizarse de una forma sencilla y rápida.
path_output = 'correlaciones.csv'
correlaciones.to_csv(path_output)
correlaciones.to_excel(path_output)
Ejemplo de uso de .corr()
Para que esté todo más claro, vamos a realizar un ejemplo con pandas.corr() para obtener las correlaciones de todas las variables:
from sklearn.datasets import load_boston
import pandas as pd
# Obtener dataframe con datos de casas (load_boston)
casas_boston = load_boston()
casas = pd.DataFrame(casas_boston.data, columns=casas_boston.feature_names)
casas['MEDV'] = casas_boston.target
# Mostramos una muestra del contenido del dataframe
print(casas.head())
# Compbrobamos el tipo de dato del dataframe. Necesitamos que todos sean numéricos.
print(casas.info())
# Obtenemos las correlaciones
print('\n------------------------------------------------------------')
print('TABLA DE CORRELACIONES con pandas .corr()')
print('------------------------------------------------------------')
print(casas.corr())
# Exportar datos a Excel
path_output = 'correlaciones.xlsx'
casas.corr().to_excel(path_output)
Y tendremos la salida siguiente tras mostrar el contenido con .head():
CRIM ZN INDUS CHAS NOX ... TAX PTRATIO B LSTAT MEDV
0 0.00632 18.0 2.31 0.0 0.538 ... 296.0 15.3 396.90 4.98 24.0
1 0.02731 0.0 7.07 0.0 0.469 ... 242.0 17.8 396.90 9.14 21.6
2 0.02729 0.0 7.07 0.0 0.469 ... 242.0 17.8 392.83 4.03 34.7
3 0.03237 0.0 2.18 0.0 0.458 ... 222.0 18.7 394.63 2.94 33.4
4 0.06905 0.0 2.18 0.0 0.458 ... 222.0 18.7 396.90 5.33 36.2
5 rows x 14 columns]
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 506 entries, 0 to 505
Data columns (total 14 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 CRIM 506 non-null float64
1 ZN 506 non-null float64
2 INDUS 506 non-null float64
3 CHAS 506 non-null float64
4 NOX 506 non-null float64
5 RM 506 non-null float64
6 AGE 506 non-null float64
7 DIS 506 non-null float64
8 RAD 506 non-null float64
9 TAX 506 non-null float64
10 PTRATIO 506 non-null float64
11 B 506 non-null float64
12 LSTAT 506 non-null float64
13 MEDV 506 non-null float64
dtypes: float64(14)
memory usage: 55.5 KB
None
------------------------------------------------------------
TABLA DE CORRELACIONES con pandas .corr()
------------------------------------------------------------
CRIM ZN INDUS ... B LSTAT MEDV
CRIM 1.000000 -0.200469 0.406583 ... -0.385064 0.455621 -0.388305
ZN -0.200469 1.000000 -0.533828 ... 0.175520 -0.412995 0.360445
INDUS 0.406583 -0.533828 1.000000 ... -0.356977 0.603800 -0.483725
CHAS -0.055892 -0.042697 0.062938 ... 0.048788 -0.053929 0.175260
NOX 0.420972 -0.516604 0.763651 ... -0.380051 0.590879 -0.427321
RM -0.219247 0.311991 -0.391676 ... 0.128069 -0.613808 0.695360
AGE 0.352734 -0.569537 0.644779 ... -0.273534 0.602339 -0.376955
DIS -0.379670 0.664408 -0.708027 ... 0.291512 -0.496996 0.249929
RAD 0.625505 -0.311948 0.595129 ... -0.444413 0.488676 -0.381626
TAX 0.582764 -0.314563 0.720760 ... -0.441808 0.543993 -0.468536
PTRATIO 0.289946 -0.391679 0.383248 ... -0.177383 0.374044 -0.507787
B -0.385064 0.175520 -0.356977 ... 1.000000 -0.366087 0.333461
LSTAT 0.455621 -0.412995 0.603800 ... -0.366087 1.000000 -0.737663
MEDV -0.388305 0.360445 -0.483725 ... 0.333461 -0.737663 1.000000
[14 rows x 14 columns]
Process finished with exit code 0
Cuando ya tenemos el conjunto de datos de correlaciones mostrado en pantalla y exportado a un archivo, vamos a descubrir cómo interpretar esos datos y para qué nos pueden servir.
Cómo interpretar los resultados de las correlaciones .corr()
La interpretación del valor de la correlación depende del contexto y del nivel de significancia estadística requerido. Sin embargo, hay algunas convenciones generales utilizadas para interpretar los valores de la correlación:- Una correlación cercana a 0: indica que no hay una relación lineal aparente entre las dos variables.
- Una correlación entre 0.3 y 0.5: se considera moderada.
- Una correlación entre 0.5 y 0.7: se considera fuerte.
- Una correlación mayor a 0.7: se considera muy fuerte.
- Todos los valores en diagonal con 1 son la línea de las mismas variables en vertical y horizontal y no deben tenerse en cuenta. Los datos se cruzan consigo mismos y de ahí la correlación del 100% entre ellas expresada como valor 1.

Los valores mostrados como -1 indican que las columnas están correlacionadas inversamente, es decir, a medida que una columna aumenta su valor en la otra disminuye y viceversa.
NOTA: recuerda que el método corr() solo funciona con datos numéricos. Si realizas la correlación con otro tipo de datos obtendrás NaN en la celda correspondiente, en cuyo caso, antes de implementarlo es conveniente aplicar los métodos dtypes o astype para convertir los valores a numéricos según sea el caso, siempre y cuando contengan números.
Siguiendo con la explicación e interpretación de los resultados de 'corr()' el ejemplo del dataset Boston, encontramos que hay algunas variables con un correlación fuerte como el caso de MEDV con RM ya que su valor es 0.695360. Dada la temática del conjunto de datos que está enfocada en el precio de la vivienda, descubrimos que cuantas más habitaciones tiene una vivienda, el precio de la misma es más elevado. Si el número de habitaciones aumenta (RM) el valor de MEDV también aumenta.
En el caso de las correlaciones inversas, podemos ver como MEDV y LSTAT están influenciadas inversamente con un valor -0.738, es decir, mostrando que el precio de la vivienda es menor cuando las personas que la habitan tienen una condición social baja. Si el valor de LSTAT aumenta el valor de MEDV disminuye. Si hay más individuos con baja condición social en la zona el precio de la vivienda cae.
En resumen, recuerda que los valores positivos en las correlaciones indican que si una variable aumenta su valor la otra lo hará también y, si el valor es negativo cuando aumenta el valor de la variable provoca que la otra variable disminuya su valor.
¿Cuándo utilizar corr?
La correlación (corr) se utiliza comúnmente en el análisis de regresión lineal antes de aplicar el modelo de regresión lineal simple y el modelo de regresión lineal múltiple. Se utiliza para determinar si hay una relación significativa entre la variable independiente (X) y la variable dependiente (Y), lo cual es una condición necesaria para aplicar uno de estos modelos de regresiones lineales.Antes de aplicar la regresión lineal es posible calcular la correlación entre la variable independiente y la variable dependiente para determinar si se debe continuar con el análisis. Si la correlación es alta y positiva, significa que hay una relación significativa entre las dos variables y se puede continuar con el análisis utilizando el modelo de regresión lineal. Si la correlación es baja o negativa, no hay una relación significativa entre las dos variables, no es necesario o no se recomienda continuar con el análisis utilizando el modelo de regresión lineal gracias a los datos mostrados con corr. Esto evitará pérdida de tiempo y costes innecesarios en desarrollos y minería de datos.
Comentarios del artículo "Correlación de variables con Pandas .corr()"
¿Te ha gustado la información? Coméntanos tus opiniones, dudas y sugerencias: