Correlación de variables con pairplot() de la librería Seaborn
Otro de los procedimientos para el análisis de datos y obtención de una matriz de correlaciones en Python consiste en usar el método pairplot() de la librería seaborn. Esta forma de conseguir las etiquetas o columnas correlacionadas dentro del conjunto de datos que utilizamos es un método gráfico, proporcionando mayor facilidad para comprender los valores ofrecidos.
Usar seaborn.pairplot() tiene ventajas e inconvenientes y, si deseas conocer todas sus características y particularidades te recomendamos que veas la explicación y los ejemplos.
Con pairplot podemos generar un diagrama de dispersión para mostrar las relaciones entre variables de un conjunto de datos. Su utilización no es demasiada compleja y, pasándole los datos mediante una matriz representará los valores de las filas y columnas correspondientes a las variables.
Otra de las ventajas de seaborn pairplot es poder crear un histograma y un gráfico de densidad para mostrar la distribución de cada variable individual con un pequeño script de Python.
Como desventajas en el uso de pairplot indicar que mostrar todas las variables al mismo tiempo en el gráfico generado puede resultar excesivo, requiriendo bastante tiempo de procesamiento y dando resultados poco analizables por el científico de datos. Añadir el conjunto de datos completo crea una imagen gráfica muy grande. Sin embargo, esto puede solucionarse fácilmente asignando un pequeño grupo de variables en cada gráfico, siendo completamente compatible con el método corr de pandas que también hemos mencionado. Generalmente se aconseja la utilización de varios métodos de correlación de variables para comparar resultados y realizar un análisis de datos más exhaustivo.
Te recomiendo que no lo ejecutes tal y como está ya que requerirá mucho tiempo en procesar todas las variables del dataset. Lo ideal, como he mencionado al inicio es seleccionar las variables que deseamos mostrar. Es perfecto elegir 5 variables o columnas del dataframe e ir haciendo pruebas de representación para obtener las relaciones deseadas o, en su defecto, utilizar primero pandas corr para descubrir las relaciones y, a partir de ahí mostrar el gráfico con pairplot con la correlaciones descubiertas.
Entonces, nos quedaríamos con el siguiente código:
Genera un dataframe que visualizamos en forma de tabla con las relaciones entre las variables. También exportamos los datos a un archivo .xlsx para guardar los resultados y poder realizar un análisis posterior en caso de necesitarlo. Recuerda que también puedes exportar los resultados a un archivo csv modificando la línea 'to_excel' por 'to_csv'.
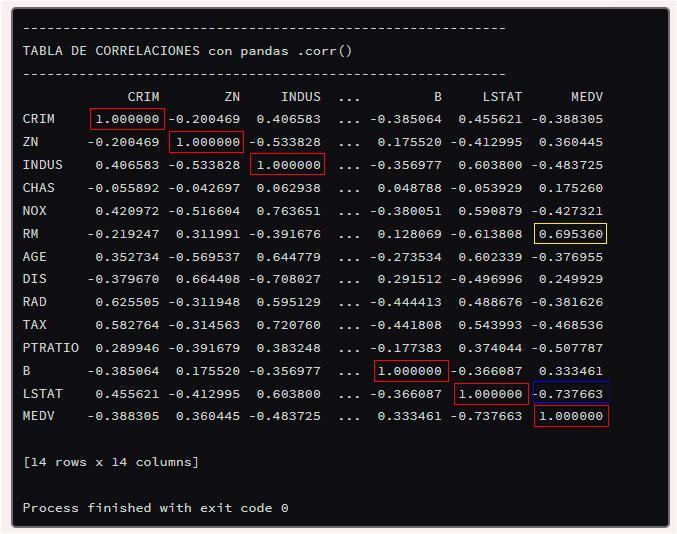
Con esto ya tenemos el archivo correlaciones_boston_corr.xlsx y los datos imprimidos por consola, así que vamos a crear el gráfico con las relaciones que hemos detectado con corr.
Cuando ejecutamos este código, obtenemos una imagen grande que contiene muchas subparcelas.
La representación gráfica de todas las variables en la matriz con pairplot resulta excesiva para una correcta visualización, por lo que optamos por elegir únicamente 5 columnas entre todas (en la vida real puedes elegir las que necesites e ir probando representaciones parciales hasta dar con las que son más interesantes). En la lista columnas se recogen los nombres de las que hemos seleccionado para el ejemplo que estamos desarrollando.
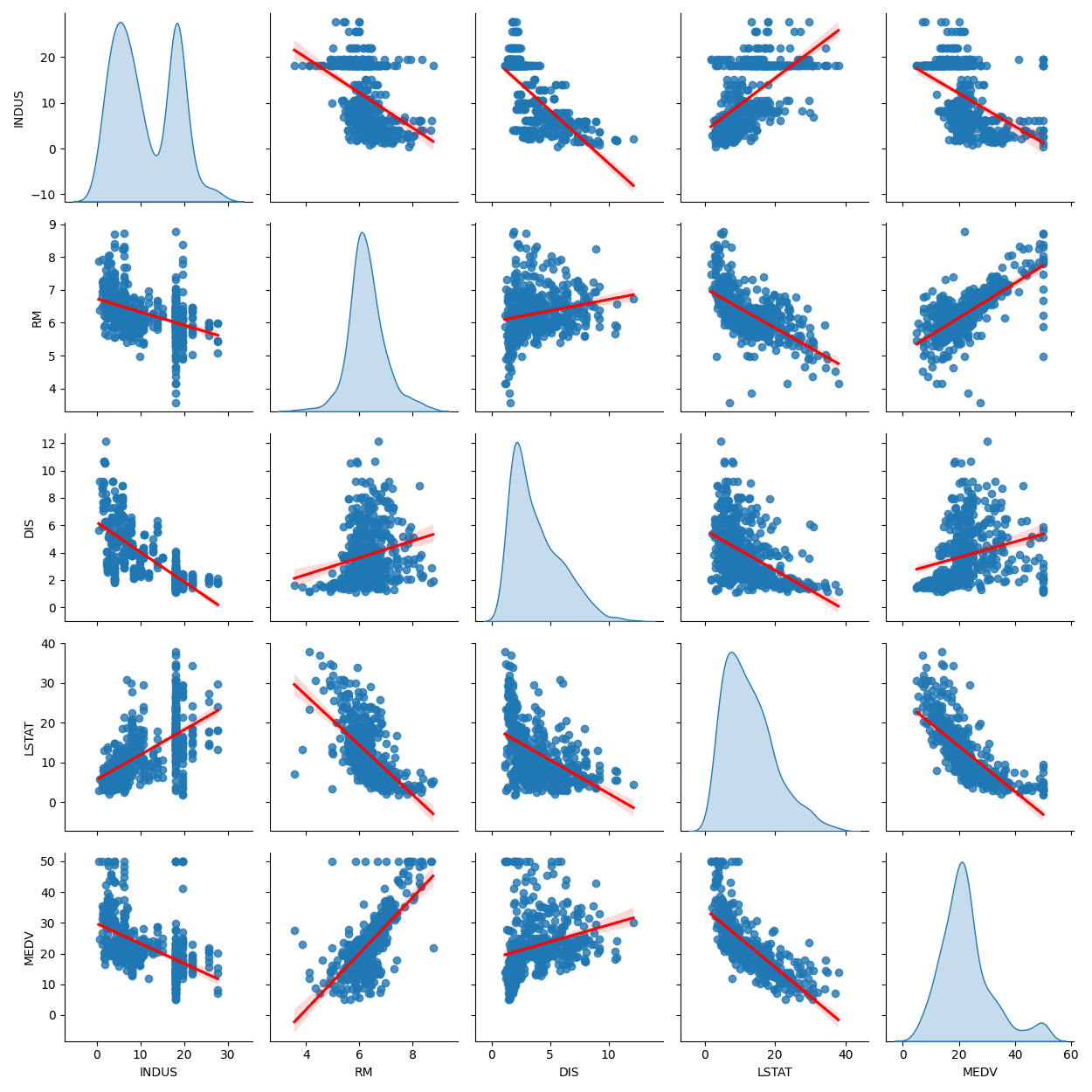
En este caso, hemos añadido, en la última línea, el método tight_layout() del módulo pyplot para ajustar los títulos de los ejes de una manera más precisa. A continuación, puedes apreciar la salida gráfica final, sobre la cual se han resaltado las representaciones que parecen confirmar la existencia de una relación lineal entre la variable independiente correspondiente y la variable MEDV.
Este código mostrará una línea diagonal en cada subfigura representada en la imagen. Para que la línea de regresión pueda verse con alto contraste cambiamos su color a rojo. Este cambio de color se realiza añadiendo plot_kws, al que debemos pasarle los valores en forma de diccionario python con la variable line_kws que contendrá el color que deseamos.
Al ejecutar generamos esta imagen:
Como dentro de este conjunto de datos no disponemos de una variable categórica, podemos crearla para mostrar cómo se vería el gráfico con distintos colores por categorías de precios. Creamos la columna 'PRICE_CAT' que obtiene el valor de 'MEDV' para asignar si es de la categoría de precio bajo, medio o alto.
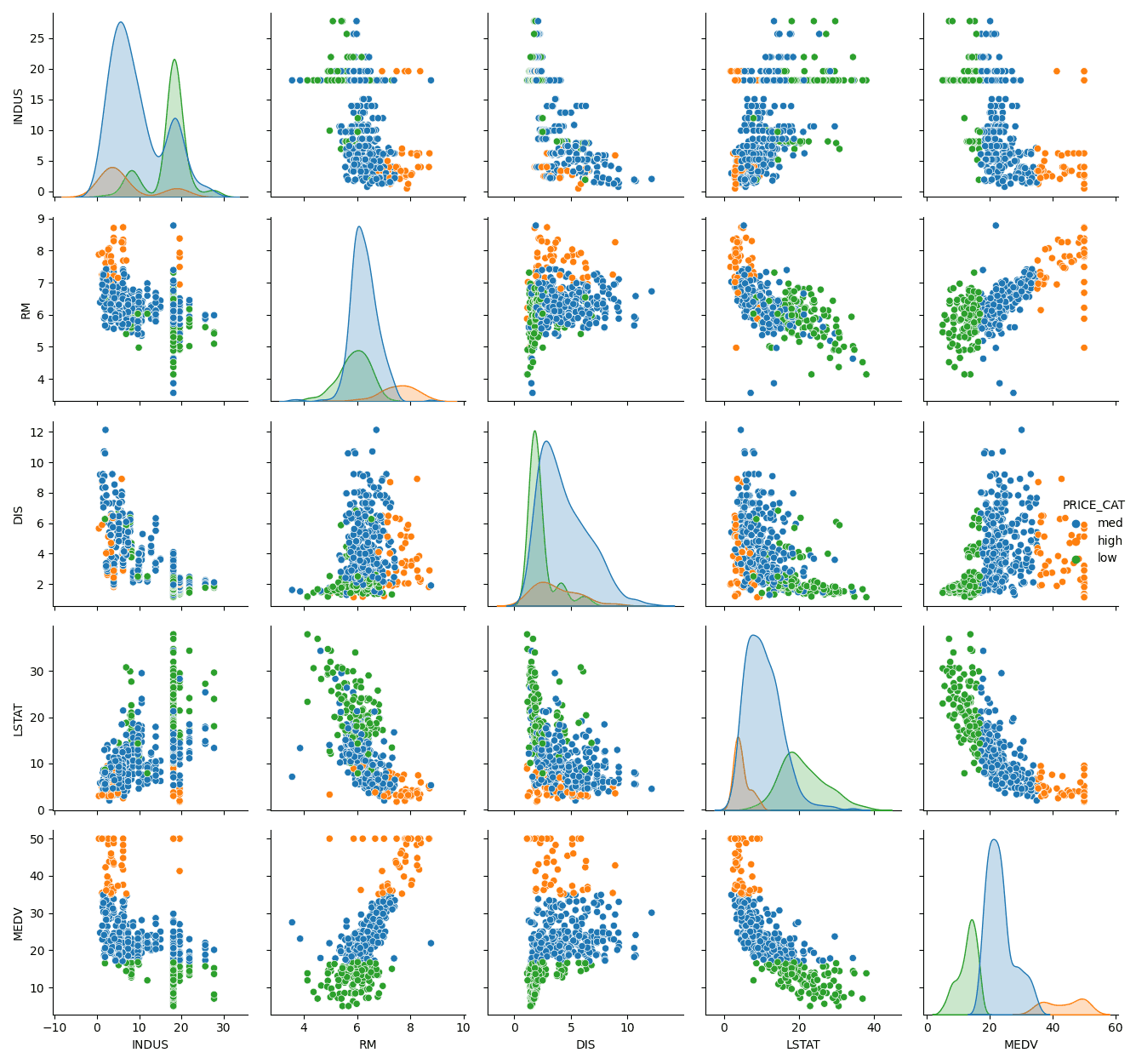
Para mostrar las categorías con distinto color con pairplot, debemos pasar la columna con las categorías mediante hue. En este caso es hue='PRICE_CAT'.
El resto del código obtiene los precios y, en función de si tiene un valor u otro asigna a la celda low, med o high.
Al ejecutar creamos la siguiente imagen.
Puedes ver más ejemplos de correlación de columnas y datos con corr y descubrir los diferentes algoritmos de aprendizaje automático supervisado.
Usar seaborn.pairplot() tiene ventajas e inconvenientes y, si deseas conocer todas sus características y particularidades te recomendamos que veas la explicación y los ejemplos.
- Índice Correlación de variables con pairplot():
¿Por qué usar pairplot de seaborn?
Existen diferentes motivos por los que utilizar el método pairplot de la biblioteca Seaborn de Python. Entre ellos destaco la visualización gráfica que mejora el análisis visual frente a otros métodos como la correlación de variables con pandas.corr() y la obtención de resultados parecidos con corrcoef().Con pairplot podemos generar un diagrama de dispersión para mostrar las relaciones entre variables de un conjunto de datos. Su utilización no es demasiada compleja y, pasándole los datos mediante una matriz representará los valores de las filas y columnas correspondientes a las variables.
Otra de las ventajas de seaborn pairplot es poder crear un histograma y un gráfico de densidad para mostrar la distribución de cada variable individual con un pequeño script de Python.
Como desventajas en el uso de pairplot indicar que mostrar todas las variables al mismo tiempo en el gráfico generado puede resultar excesivo, requiriendo bastante tiempo de procesamiento y dando resultados poco analizables por el científico de datos. Añadir el conjunto de datos completo crea una imagen gráfica muy grande. Sin embargo, esto puede solucionarse fácilmente asignando un pequeño grupo de variables en cada gráfico, siendo completamente compatible con el método corr de pandas que también hemos mencionado. Generalmente se aconseja la utilización de varios métodos de correlación de variables para comparar resultados y realizar un análisis de datos más exhaustivo.
Cómo crear un gráfico de correlación en Python con pairplot seaborn
Con este sencillo script de python podemos obtener los datos del dataset de skelearn llamado Boston y generar un gráfico de correlación de variables con pairplot.
import seaborn as sns
from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
import pandas as pd
# Cargar los datos en un DataFrame de pandas (en este caso usamos dataset boston)
boston_data = load_boston()
boston = pd.DataFrame(boston_data.data, columns=boston_data.feature_names)
# Crear un gráfico de correlación utilizando pairplot
sns.pairplot(boston)
# Mostrar el gráfico
plt.show()
Entonces, nos quedaríamos con el siguiente código:
import seaborn as sns
from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
import pandas as pd
# Cargar los datos en un DataFrame de pandas (en este caso usamos dataset boston)
boston_data = load_boston()
boston = pd.DataFrame(boston_data.data, columns=boston_data.feature_names)
print('\nContenido dataset Boston original (5 filas de muestra):')
print('---------------------------------')
print(boston.head())
print('\nNombres de las columnas del dataset boston:')
print('---------------------------------')
print(boston_data.feature_names)
#-----------------------------------------------------------------------------------------------------------------
# Añadir columna (MEDV) al dataframe
# MEDV: mediana de los valores de las viviendas ocupadas por las personas propietarias (en unidades de mil dólares).
# Esta variable está asociada a la clave target. Lo habitual es usar MEDV como variable dependiente (y).
# La mediana de un conjunto es el valor que ocupa la posición intermedia, es decir, la mitad de los términos son
# superiores y la otra mitad son inferiores.
# Mediana del conjunto = Suma de los números / cantidad de números
#-----------------------------------------------------------------------------------------------------------------
boston['MEDV'] = boston_data.target
print('\nContenido dataframe boston con columna (MEDV) añadida:')
print('---------------------------------')
print(boston.head())
- Las importaciones de las bibliotecas de Python que vamos a utilizar están en las primeras líneas.
- Seguidamente cargamos el dataset Boston con los datos recopilados por la Universidad Carnegie Mellon y lo asignamos a un dataframe de pandas. Puedes utilizar cualquier otro conjunto de datos, pero para realizar nuestros primeros análisis y regresiones son bastante útiles. Incluso es opcional cargar un dataset con datos propios.
- Mostramos una muestra del contenido del dataframe que hemos creado con el método head(). Este imprime las 5 primeras filas de datos. Si en lugar de 5 filas deseas mostrar otro número de filas, simplemente añade el número a head así: 'boston.head(num_filas).
- Imprimimos el nombre de las columnas con 'boston_data.feature_names'.
- Añadir la columna 'MEDV' al dataframe es muy importante. Esta contiene la mediana de precios de las viviendas. El inconveniente de usar conjuntos de datos ya creados es que estos no siempre están como deseamos, o más bien no conocemos su estructura de antemano y, en el caso del dataset boston tiene algunas particularidades, como disponer el precio de las viviendas en otro campo llamado 'MEDV' que debemos obtener y añadir al dataframe como variable dependiente (y) que compone el conjunto de datos completo. Hemos añadido la nueva columna con:
- boston['MEDV'] = boston_data.target.
- Indicamos que en el dataframe llamado Boston, añada una columna con nombre MEDV con los datos procedentes de boton_data.target.
Método corr() para descubrir relaciones en columnas del dataframe
Para no saturar el ordenador, primero vamos a obtener las correlaciones con pandas.corr. De esta forma veremos con facilidad las columnas que más nos interesan del conjunto de datos que estamos analizando.
# Correlación de variables con pandas.corr
print(boston.corr())
# Exportar datos a Excel
path_output = 'correlaciones_boston_corr.xlsx'
boston.corr().to_excel(path_output)
Con esto ya tenemos el archivo correlaciones_boston_corr.xlsx y los datos imprimidos por consola, así que vamos a crear el gráfico con las relaciones que hemos detectado con corr.
Usar seaborn pairplot para crear gráfico de correlaciones
Podemos enviar a 'pairplot' todo el conjunto de variables (columnas) del dataframe para que genere la imagen correspondiente, pero esto saturaría el ordenador o ralentizaría el proceso enormemente. En su lugar, tomaremos las 5 variables con mayor correlación para mostrar en el gráfico las correlaciones con pairplot. Estas variables las hemos descubierto previamente con corr, y son las que nos interesan debido a su interacción. Si el valor de una aumenta o disminuye también lo harán los valores de las otras de forma con una correlación positiva si los valores de corr() son positivos o negativa si los valores indicados por corr() son negativos.Seleccionar columnas del dataframe para pairplot
columnas = ['INDUS', 'RM', 'DIS', 'LSTAT', 'MEDV']
sns.pairplot(boston[columnas], height=2.5)
plt.tight_layout()
plt.show()
La representación gráfica de todas las variables en la matriz con pairplot resulta excesiva para una correcta visualización, por lo que optamos por elegir únicamente 5 columnas entre todas (en la vida real puedes elegir las que necesites e ir probando representaciones parciales hasta dar con las que son más interesantes). En la lista columnas se recogen los nombres de las que hemos seleccionado para el ejemplo que estamos desarrollando.En este caso, hemos añadido, en la última línea, el método tight_layout() del módulo pyplot para ajustar los títulos de los ejes de una manera más precisa. A continuación, puedes apreciar la salida gráfica final, sobre la cual se han resaltado las representaciones que parecen confirmar la existencia de una relación lineal entre la variable independiente correspondiente y la variable MEDV.
Contenido de las columnas del dataframe para pairplot
- CRIM: tasa de delincuencia per cápita asociada a cada observación.
- ZN: porcentaje de zonas residenciales (para terrenos con un área por encima de las 25 mil pulgadas cuadradas).
- INDUS: porcentaje de negocios que no sean de comercio al por menor (relacionado con el nivel de industrialización de la zona).
- CHAS: variable ficticia o dummy introducida en el sistema con fines discriminatorios. En nuestro caso, vale 1 si el tramo en el que se encuadra la observación tiene salida hacia el río y cero (0) si no tiene salida al río.
- NOX: concentración de óxido nítrico (en partes por 10 millones).
- RM: número medio de habitaciones por vivienda en la observación realizada.
- AGE: porcentaje de viviendas ocupadas por la persona propietaria y construidas con anterioridad a 1940.
- DIS: valores de las distancias a 5 centros de trabajo de la ciudad de Boston (dichos valores se encuentran ponderados).
- RAD: índice que mide el nivel de accesibilidad a una vía de alta velocidad (autovía, autopista…) que permite conectar con otra población.
- TAX: tasa impositiva sobre la propiedad (en unidades de 10 mil dólares).
- PTRATIO: ratio estudiantes-docentes asociado a cada medición.
- B: término que, a través de una fórmula, cuantifica la proporción de personas con raíces afro-americanas.
- LSTAT: proporción de individuos de baja condición social en la zona en la que se realiza la medición.
- MEDV: mediana de los valores de las viviendas ocupadas por las personas propietarias (en unidades de mil dólares). Esta variable está asociada a la clave target. Lo habitual es usar MEDV como variable dependiente.
Línea de regresión en pairplot
Si queremos identificar las relaciones de los datos en el diagrama de dispersión creado con pairplot, podemos añadir la línea de regresión con king='reg'. En ese caso haríamos lo siguiente:
sns.pairplot(
boston[columnas], kind='reg', diag_kind='kde', plot_kws={'line_kws': {'color': 'red'}}
)
plt.tight_layout()
plt.show()
Al ejecutar generamos esta imagen:
Añadir color a cada categoría
Si disponemos de una variable categórica dentro del conjunto de datos, también es posible usarla para mostrar cada categoría con un color diferente. De esta forma, visualizaremos de manera óptima dónde se posicionan los elementos pertenecientes a cada una de ellas. Este es un método visualmente mejor para mostrar gráficos y ver las distribuciones y tendencias de cada categoría.
# ------------------------------------------------------------------------------------------------------------
# Nueva columna llamada PRICE_CAT en la que añadimos low, med o high según el precio de la vivienda.
# ------------------------------------------------------------------------------------------------------------
# Añadir categoría por precio:
# De 0 a 17.0 = precio bajo (low)
# De 17.0 a 34.9 = precio medio (med)
# Superior a 35.0 = precio alto (high)
# ------------------------------------------------------------------------------------------------------------
PRICE_CAT = []
for row in boston['MEDV']:
if row <= 17.0: PRICE_CAT.append('low')
elif row > 17.0 and row < 35.0: PRICE_CAT.append('med')
elif row >= 35.0: PRICE_CAT.append('high')
else: PRICE_CAT.append('Not_Rated')
boston['PRICE_CAT'] = PRICE_CAT
# obtenemos un gráfico con un color para cada categoría dentro de la variable asignada a hue.
# Los puntos más oscuros indican un precio más alto de las viviendas, valorando la columna indicada, es decir,
# valoraría: MDEV e INDUS, MEDV y RM, MEDV y DIS, MEDV y LSTAT y así con todas las variables o columnas pasadas a pairplot.
columnas = ['INDUS', 'RM', 'DIS', 'LSTAT', 'MEDV', 'PRICE_CAT']
sns.pairplot(
boston[columnas], hue='PRICE_CAT',
)
plt.tight_layout()
plt.show()
Para mostrar las categorías con distinto color con pairplot, debemos pasar la columna con las categorías mediante hue. En este caso es hue='PRICE_CAT'.
El resto del código obtiene los precios y, en función de si tiene un valor u otro asigna a la celda low, med o high.
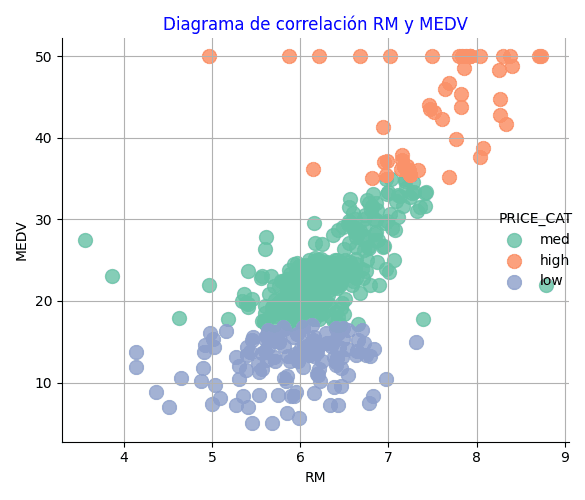
Diagrama de correlación lmplot entre dos variables
También podemos obtener de forma visual el diagrama de correlación de dos variables, mostrando las categorías con distinto color siguiendo el ejemplo anterior:
columnas = ['RM', 'MEDV', 'PRICE_CAT']
sns.lmplot(
data=boston, x='RM', y='MEDV',
hue='PRICE_CAT',
palette='Set2',
fit_reg=False,
scatter_kws={'s': 100}
)
plt.grid()
plt.title("Diagrama de correlación RM y MEDV", color='blue')
plt.tight_layout()
plt.show()
Código completo Correlación de variables con Seaborn pairplot()
Aquí está el código completo para crear gráficos con seaborn y pairplot y descubrir las relaciones entre columnas de un dataframe.
import seaborn as sns
from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
import pandas as pd
# Cargar los datos en un DataFrame de pandas (en este caso usamos dataset Boston)
boston_data = load_boston()
boston = pd.DataFrame(boston_data.data, columns=boston_data.feature_names)
print('\nContenido dataset Boston original (5 filas de muestra):')
print('---------------------------------')
print(boston.head())
print('\nNombres de las columnas del dataset Boston:')
print('---------------------------------')
print(boston_data.feature_names)
# -----------------------------------------------------------------------------------------------------------------
# Añadir columna (MEDV) al dataframe
# MEDV: mediana de los valores de las viviendas ocupadas por las personas propietarias (en unidades de mil dólares).
# Esta variable está asociada a la clave target. Lo habitual es usar MEDV como variable dependiente (y).
# La mediana de un conjunto es el valor que ocupa la posición intermedia, es decir, la mitad de los términos son
# superiores y la otra mitad son inferiores.
# Mediana del conjunto = Suma de los números / cantidad de números
# -----------------------------------------------------------------------------------------------------------------
boston['MEDV'] = boston_data.target
print('\nContenido dataframe boston con columna (MEDV) añadida:')
print('---------------------------------')
print(boston.head())
# Correlación de variables con pandas.corr
print(boston.corr())
# Exportar datos a Excel
path_output = 'correlaciones_boston_corr.xlsx'
boston.corr().to_excel(path_output)
# Crear gráfico con pairplot con las variables relevantes
columnas = ['INDUS', 'RM', 'DIS', 'LSTAT', 'MEDV']
sns.pairplot(boston[columnas], height=2.5)
plt.tight_layout()
plt.show()
# ------------------------------------------------------------------------------------------------------------
# Al ejecutar este código, nos muestra el gráfico de pares de Seaborn con la estimación de densidad a lo largo de la # diagonal.
# Si queremos identificar las relaciones de los datos en el diagrama de dispersión, podemos añadir
# una línea de regresión con king='reg'.
# Esto motrará una línea en la diagonal de cada subfigura representada en la imagen.
# Para que la línea de regresión pueda verse con alto contraste, cambiamos el color a rojo.
# Este cambio de color se realiza añadiendo plot_kws, al que debemos pasarle los valores en forma de diccionario python
# con la variable line_kws que contendrá el color que deseamos.
# ------------------------------------------------------------------------------------------------------------
# Usar plot_kws para cambiar el color de la línea de regresión
sns.pairplot(
boston[columnas], kind='reg', diag_kind='kde', plot_kws={'line_kws': {'color': 'red'}}
)
plt.tight_layout()
plt.show()
# ------------------------------------------------------------------------------------------------------------
# Nueva columna llamada PRICE_CAT en la que añadimos low, med y high según el precio de la vivienda.
# ------------------------------------------------------------------------------------------------------------
# Añadir categoría por precio:
# De 0 a 17 = precio bajo (low)
# De 18 a 34 = precio medio (med)
# Superior a 35 = precio alto (high)
# ------------------------------------------------------------------------------------------------------------
PRICE_CAT = []
for row in boston['MEDV']:
if row <= 17.0: PRICE_CAT.append('low')
elif row > 17.0 and row < 35.0: PRICE_CAT.append('med')
elif row >= 35.0: PRICE_CAT.append('high')
else: PRICE_CAT.append('Not_Rated')
boston['PRICE_CAT'] = PRICE_CAT
# obtenemos un gráfico con un color para cada categoría dentro de la variable asignada a hue.
# Los puntos más oscuros indican un precio más alto de las viviendas, valorando la columna indicada, es decir,
# valoraría: MDEV e INDUS, MEDV y RM, MEDV y DIS, MEDV y LSTAT y así con todas las variables o columnas pasadas a pairplot.
columnas = ['INDUS', 'RM', 'DIS', 'LSTAT', 'MEDV', 'PRICE_CAT']
sns.pairplot(
boston[columnas], hue='PRICE_CAT',
)
plt.tight_layout()
plt.show()
columnas = ['RM', 'MEDV', 'PRICE_CAT']
sns.lmplot(
data=boston, x='RM', y='MEDV',
hue='PRICE_CAT',
palette='Set2',
fit_reg=False,
scatter_kws={'s': 100}
)
plt.grid()
plt.title("Diagrama de correlación RM y MEDV", color='blue')
plt.tight_layout()
plt.show()
Comentarios del artículo "Correlación de variables con pairplot() de la librería Seaborn"
¿Te ha gustado la información? Coméntanos tus opiniones, dudas y sugerencias: